104. Maximum Depth of Binary Tree

Leetcode

https://leetcode.com/problems/maximum-depth-of-binary-tree/

題目

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

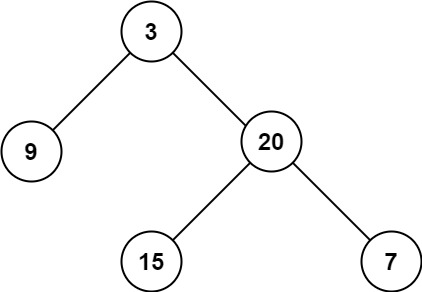
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

解答

• 方法一

Recursion (DFS)

var maxDepth = function(root) {
    if(!root) return 0;
    
    const children = [root.left, root.right];
    if(children.every(child => !child)) {
        return 1;
    }
    
    let depth = 0;
    children.forEach(child => {
        depth = Math.max(depth, maxDepth(child));
    })
    
    return depth + 1;
};

Runtime: 80 ms, faster than 73.62% of JavaScript online submissions for Maximum Depth of Binary Tree.

Memory Usage: 47.3 MB, less than 5.07% of JavaScript online submissions for Maximum Depth of Binary Tree.

• 方法二

Recursion (DFS)

比較左右兩邊子樹的高度，取其最高再加上本身的高度 1

var maxDepth = function(root) {
    if (!root) return 0;
    
    const leftH = maxDepth(root.left);
    const rightH = maxDepth(root.right);
    
    return Math.max(leftH, rightH) + 1;
};

Runtime: 91 ms, faster than 57.09% of JavaScript online submissions for Maximum Depth of Binary Tree.

Memory Usage: 44.8 MB, less than 83.64% of JavaScript online submissions for Maximum Depth of Binary Tree.

• 方法三

Recursion (DFS) - 尾遞歸

方法二的優化

var maxDepth = function(root) {
    const helper = (node, totalDepth) => {
        if (!node) return totalDepth;
        const leftH = helper(node.left, totalDepth + 1);
        const rightH = helper(node.right, totalDepth + 1);
        
        return Math.max(leftH, rightH);
    }
    
    return helper(root, 0);
};

Runtime: 72 ms, faster than 86.13% of JavaScript online submissions for Maximum Depth of Binary Tree.

Memory Usage: 45.1 MB, less than 68.36% of JavaScript online submissions for Maximum Depth of Binary Tree.

• 方法四

Iteration (DFS)

var maxDepth = function(root) {
    if(!root) return 0;
    
    let ans = 0;
    const stack = [{
        node: root,
        depth: 1
    }]
    while (stack.length) {
        const curr = stack.pop();
        const node = curr.node;
        const depth = curr.depth;
        
        const children = [node.left, node.right];
        if(children.every(child => !child)) {
            ans = Math.max(ans, depth)
        }
        children.forEach(child => {
            if(child) {
                stack.push({
                    node: child,
                    depth: depth + 1
                })
            }
        })
    }
    
    return ans;
};

Runtime: 76 ms, faster than 78.84% of JavaScript online submissions for Maximum Depth of Binary Tree.

Memory Usage: 46.8 MB, less than 5.07% of JavaScript online submissions for Maximum Depth of Binary Tree.

• 方法五

Iteration (BFS)

var maxDepth = function(root) {
    if (!root) return 0;
    
    let ans = 0;
    const queue = [{
        node: root,
        depth: 1
    }];
    
    while(queue.length) {
        const curr = queue.shift();
        const node = curr.node;
        const depth = curr.depth;
        
        const children = [node.left, node.right];
        if(children.every(child => !child)) {
            ans = Math.max(ans, depth);
        }
        children.forEach(child => {
            if(child) queue.push({
                node: child,
                depth: depth + 1
            })
        })
    }
    
    return ans;
};

Runtime: 84 ms, faster than 68.47% of JavaScript online submissions for Maximum Depth of Binary Tree.

Memory Usage: 46.6 MB, less than 5.49% of JavaScript online submissions for Maximum Depth of Binary Tree.