98. Validate Binary Search Tree

Leetcode

https://leetcode.com/problems/validate-binary-search-tree/

題目

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.

• The right subtree of a node contains only nodes with keys greater than the node's key.

• Both the left and right subtrees must also be binary search trees.

Example 1:

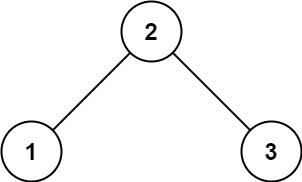
Input: root = [2,1,3]
Output: true

Example 2:

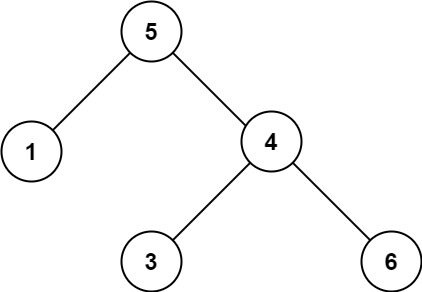
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

解答

• 方法一

dfs preorder

在每一個節點中往上傳 isValid, min, max，每個節點再跟左右節點的最大最小值比較看是否為 isValid

var isValidBST = function(root) {
    const preOrder = (node) => {
        if (!node) {
            return {
                isValid: true,
                min: Number.MAX_SAFE_INTEGER,
                max: Number.MIN_SAFE_INTEGER
            }
        }
        
        const val = node.val;
        if(!node.left && !node.right) {
            return {
                isValid: true,
                min: val,
                max: val
            }
        }
        
        const left = preOrder(node.left);
        const right = preOrder(node.right);
        if (!left.isValid || !right.isValid) {
            return {
                isValid: false,
            }
        }
        return {
            isValid: val > left.max && val < right.min,
            min: Math.min(val, left.min, right.min),
            max: Math.max(val, left.max, right.max)
        }
    }
    
    return preOrder(root).isValid;
};

Runtime: 156 ms, faster than 5.10% of JavaScript online submissions for Validate Binary Search Tree.

Memory Usage: 47.7 MB, less than 7.92% of JavaScript online submissions for Validate Binary Search Tree.

• 方法二

DFS preorder

在遍歷每一個節點時，檢查其值是否在上下限的範圍中 (low: 下限、high: 上限)

Example 2.

5 => low: 負無限大, high: 正無限大

1 => low: 負無限大, high: 5

4 => low: 5, high: 正無限大 => isValid === false

3 => low: 負無限大, high: 4

6 => low: 4, high: 正無限大

var isValidBST = function(root) {
    const preOrder = (node, low, high) => {
        if (!node) return true;
        
        const val = node.val;
        
        // 左邊子節點的上限值為 原本的 high 值與本身節點的值取最小值
        const isLeftValid = preOrder(node.left, low, Math.min(val, high));
        // 右邊子節點的下限值為 原本的 low 值與本身節點的值取最大值
        const isRightValid = preOrder(node.right, Math.max(val, low), high);
        
        if (!isLeftValid || !isRightValid) return false;
        if (val >= high) return false;
        if (val <= low) return false;
        return true;
    }
    
    return preOrder(root, Number.MIN_SAFE_INTEGER, Number.MAX_SAFE_INTEGER);
};

Runtime: 56 ms, faster than 99.72% of JavaScript online submissions for Validate Binary Search Tree.

Memory Usage: 46.3 MB, less than 54.66% of JavaScript online submissions for Validate Binary Search Tree.

• 方法三

BFS preorder

用 stack 採用先右後左 push 的方式

var isValidBST = function(root) {
    const stack = [{
        node: root,
        low: Number.MIN_SAFE_INTEGER,
        high: Number.MAX_SAFE_INTEGER,
    }]
    
    while(stack.length) {
        const {node, low, high} = stack.pop();
        // 空節點直接略過檢查
        if (!node) continue;
        
        const val = node.val;
        
        // 先右後左 push => preorder
        stack.push({
            node: node.right,
            low: Math.max(val, low),
            high
        });
        stack.push({
            node: node.left,
            low,
            high: Math.min(val, high)
        });
        
        if (val >= high || val <= low) return false;
    }
    return true;
};

Runtime: 98 ms, faster than 52.66% of JavaScript online submissions for Validate Binary Search Tree.

Memory Usage: 46.9 MB, less than 16.01% of JavaScript online submissions for Validate Binary Search Tree.

• 方法四

DFS inorder

採用 inorder 的好處就是只要判斷每個元素的值都大於前一個元素就好

Ex.

input => [4, 2, 5, 1, 6]

after inorder => [1, 2, 6, 4, 5]

這時只要判斷是不是每個元素的值都大於前一個 => 發現 6 大於 4 => isValid === false

var isValidBST = function(root) {
    let prev = Number.MIN_SAFE_INTEGER;
    
    const inorder = (node) => {
        if (!node) return true;
        if (!inorder(node.left)) return false;
        
        // 中間的元素每次都會在判斷完之後，成為前一個元素與右邊節點比較
        if (node.val <= prev) return false;
        prev = node.val;
        
        if (!inorder(node.right)) return false;
        return true;
    }
    
    return inorder(root);
};

Runtime: 60 ms, faster than 99.37% of JavaScript online submissions for Validate Binary Search Tree.

Memory Usage: 46.1 MB, less than 81.02% of JavaScript online submissions for Validate Binary Search Tree.

• 方法五

BFS inorder

var isValidBST = function(root) {
    let prev = Number.MIN_SAFE_INTEGER;
    const stack = [];
    
    // 一開始的時候要加入 root 為 true 的判斷
    while (stack.length || root) {
        // 指向樹最左邊的節點，並把路上的節點依序 push 到 stack 中
        while (root) {
            stack.push(root);
            root = root.left;
        }
        
        root = stack.pop();
        
        if (root.val <= prev) return false;
        
        // 目前節點變成前一個節點
        prev = root.val;
        
        // root 指向下一個右節點
        root = root.right;
    }
    
    return true;
};

Runtime: 142 ms, faster than 8.16% of JavaScript online submissions for Validate Binary Search Tree.

Memory Usage: 46.6 MB, less than 34.92% of JavaScript online submissions for Validate Binary Search Tree.