11. Container With Most Water

Leetcode

https://leetcode.com/problems/container-with-most-water/description/

題目

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

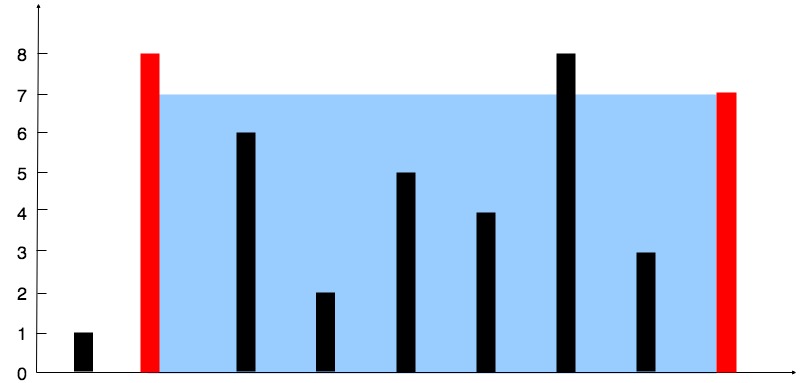
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1]
Output: 1

解答

• 方法一 - 暴力解

var maxArea = function (height) {
    let max = 0;

    for (let i = 0; i < height.length; i++) {
        for (let j = i + 1; j < height.length; j++) {
            max = Math.max(max, Math.min(height[i], height[j]) * (j - i));
        }
    }

    return max;
};

Time Limit Exceeded

• 方法二

以 example 1. 的範例來看：height = [1,8,6,2,5,4,8,3,7]

我們希望中間圍出的面積最大，一開始先從寬度最大來看，也就是取 最左(left) 及 最右(right) 的數值進行計算

1. 第一輪 - left = 0, height[0] = 1, right = 8, height[8] = 7

   中間圍出的面積 = Math.min(height[0], height[8]) * (right - left) = 7

   接著因為中間柱子的高度也有可能高到即使寬度減少了，能圍出來的面積也可以大於 7，所以下一步需要思考的是此時如果要縮小寬度，那要往那邊縮呢？很明顯的一定是比較左右柱子的高度，移動高度矮的那邊，希望他能變得更高，接續看寬度縮小後中間圍出來的面積是否會變大，所以第二輪要移動的是左邊的柱子

2. 第二輪 - left = 1, height[1] = 8, right = 8, height[8] = 7

   中間圍出的面積 = Math.min(height[1], height[8]) * (right - left) = 49

   因為目前右邊的柱子比較矮，所以接著第三輪需要移動的是右邊的柱子

3. 第三輪 - left = 1, height[1] = 8, right = 7, height[7] = 3

   中間圍出的面積 = Math.min(height[1], height[7]) * (right - left) = 18

......

接著我們就一路這樣移動，直到左邊的柱子遇到右邊的柱子為止，每輪紀錄可能圍出的最大面積就是答案

var maxArea = function (height) {
    let max = 0;

    let left = 0;
    let right = height.length - 1;
    while (left < right) {
        // 計算目前中間圍出來的面積
        max = Math.max(max, Math.min(height[left], height[right]) * (right - left));
        if (height[left] < height[right]) {
            left++
        } else {
            right--;
        }
    }

    return max;
};